자료구조_Ch 5. Binary Search Tree(이진탐색트리)

모든 원소는 서로 다른 유일한 키를 갖는다.

• 왼쪽 서브트리에 있는 원소의 키들은 그 루트의 키보다 작다.
• 오른쪽 서브트리에 있는 원소의 키들은 그 루트의 키보다 크다.
• 왼쪽 서브트리와 오른쪽 서브트리도 이진 탐색 트리이다. 
• 왼쪽 서브트리와 오른쪽 서브트리도 이진 탐색 트리이다. 
• 11 을 탐색한다면 ...  
• 탐색 회수는  

탐색 회수

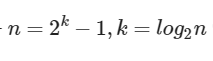
• 이진탐색트리를 이용해 TreeSort를 할 수 있다. inOrder Algorithm을 이용하면 된다.
• -> 중위순위를 이용하여 TreeSort를 할 수 있음.
• 최소값은 왼쪽으로 탐색해서 마지막 노드이고 최대값은 우측으로 탐색해서 마지막 값이다.
• 
• 이진탐색트리 ADT
  • root = BNode(), BNode는 item과 left, right 를 가지는 객체다.
  • search method: root 부터 item이 root값보다 작으면 왼쪽으로, 크면 오른쪽으로 이동하면서 탐색한다. 탐색에 성공하면 해당노드를 리턴하고 실패하면 None을 리턴한다.
  • insert method: 삽입은 탐색한 후, 실패한 위치에 삽입한다.
  • inOrder method: 중위탐색을 실행하여 트리로부터 정렬된 결과를 리턴한다.
  • minimum method: 트리의 최소값을 찾는다. 최소값은 왼쪽으로 내려 가다가 None을 만났을 때 부모노드의 값이다.
  • delMin method: 트리의 최소노드를 삭제한다.
  • delete Method: 특정 값을 가지는 노드를 삭제한다.
    삭제연산은 세가지 경우가 존재한다.
    • 1) 삭제할 노드가 단말노드인 경우: 해당 노드를 삭제한다

    • 

    • 2) 삭제할 노드가 하나의 자식노드를 가진 경우: 해당노드를 삭제하고 자식노드를 자신의 부모노드에 연결한다.

    • 

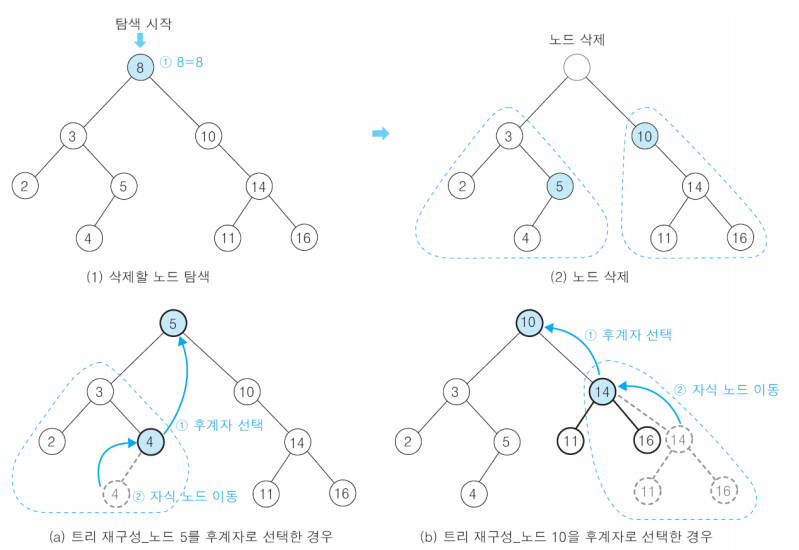
    • 3) 삭제할 노드가 두개의 자식노드를 가진 경우: 삭제할 노드 우측노드 중 최소값을 가지는 노드를 후계자 노드로 지정한다. 후계자 노드를 삭제노드로 옮기고 이진탐색트리 재구성 작업을 실행한다.
    • 

    • class BNode:
          def __init__(self, item, left=None, right=None):
              self.item = item
              self.left = left
              self.right = right
      
      class BSTree: #이진탐색트리 : Binary Search Tree
          def __init__(self):
              self.root = None
      
          def insert(self, item):  # item을 삽입한다.
              #self.root = self._insert(self.root, item)
      
          def _insert(self, curNode, item):
              # curNode 부터 밑으로 item 삽입위치를 찾아 삽입한다.
              # 현재 노드가 None이면 현재노드에 새노드를 삽입한다.
              if curNode == None:
                  curNode = BNode(item)
              elif item < curNode.item:
              # 삽입할 값이 현재 노드값 보다 작으면 좌측을 현재노드로 보고 삽입을 실행한다.
                  curNode.left = self._insert(curNode.left, item)
              else:
              # 삽입할 값이 현재 노드값 보다 크면 우측을 현재노드로 보고 삽입을 실행한다.
                  curNode.right = self._insert(curNode.right, item)
              # 재귀가 끝나서 새노드를 삽입했다면 자신을 호출한 프로세스에 새노드를 리턴한다.
              return curNode
          
          def inOrder(self):
              return self._inOrder(self.root)
      
          def _inOrder(self, node, sorted=[]):
              # 현재 노드가 비어있지 않으면 일단, 계속 좌측으로 간다. 좌측의 끝에 도달하면 노드를 출력하고 오른쪽으로 이동한다.
              if node is not None:
                  self._inOrder(node.left, sorted)
                  sorted.append(node.item)
                  self._inOrder(node.right, sorted)
              return sorted
      
          def levelOrder(self):
              h = self.height(self.root) # 트리의 높이를 계산
              for i in range(1, h + 1): # Level 1, 2, ... 순으로 내려가면서 
                  self._levelOrder(self.root, i)
                  print()
      
          def _levelOrder(self, node, level):
              if node is None:
                  return
              if level == 1:
                  print(node.item, end=" ")
              elif level > 1: # 하나씩 내려가면서 level을 낮춘다. level이 1이 되는 순간 프린트
                  self._levelOrder(node.left, level - 1)
                  self._levelOrder(node.right, level - 1)
      
          def height(self, node):
              if node is None:
                  return 0
              else:
                  # Compute the height of each subtree
                  lheight = self.height(node.left)
                  rheight = self.height(node.right)
      
                  # Use the larger one
                  if lheight > rheight:
                      return lheight + 1
                  else:
                      return rheight + 1
                  
                  
      a = [50, 30, 80, 10, 40, 90]
      t = BSTree()
      for val in a:
          t.insert(val)
      t.insert(35)
      print(t.inOrder())
      print(t.levelOrder())

• 탐색 알고리즘
  • 아래 트리에서 40을 탐색한다고 하자. 
  • step 1: 루트부터 아이템을 찾는다. return self._search(self.root, item)
    step 2: curNode = self.root
    만약, curNode.item > item 이면 왼쪽으로 curNode를 바꾸고 반대로 curNode.item < item 이면 오른쪽으로 curNode를 바꾸고 찾는다.
    움직이면서 curNode.item == item 으로 노드를 찾으면 해당 노드를 리턴한다. curNode == None 이면 찾는 노드가 없는 것이므로 에러 메세지를 출력한다.
    step 3: 움직일 때 마다 return 문에 의해 자신을 호출한 재귀프로세스에 최종적으로 찾은 item을 리턴해야 한다. 리턴이 없으면 찾아도 리턴되지 않으므로 재귀를 끝낼때 찾은 노드를 확인할 수 없다.

  • class BNode:
        def __init__(self, item):
            self.item = item
            self.left = None
            self.right = None
    
        def setLeft(self, node):
            self.left = node
    
        def setRight(self, node):
            self.right = node
    
    
    class BSTree:
        def __init__(self):
            self.root = None
    
        def insert(self, item):  # item을 삽입한다.
            self.root = self._insert(self.root, item)
    
        def _insert(self, curNode, item):
            # curNode 부터 밑으로 item 삽입위치를 찾아 삽입한다.
            # 현재 노드가 None이면 현재노드에 새노드를 삽입한다.
            if curNode == None:
                curNode = BNode(item)
            elif item < curNode.item:
            # 삽입할 값이 현재 노드값 보다 작으면 좌측을 현재노드로 보고 삽입을 실행한다.
                curNode.left = self._insert(curNode.left, item)
            else:
            # 삽입할 값이 현재 노드값 보다 크면 우측을 현재노드로 보고 삽입을 실행한다.
                curNode.right = self._insert(curNode.right, item)
            # 재귀가 끝나서 새노드를 삽입했다면 자신을 호출한 프로세스에 새노드를 리턴한다.
            return curNode
        
        def search(self, item):
            # 루트부터 item을 찾는다.
            return self._search(self.root, item)
    
        def _search(self, curNode, item):
            # curNode 밑에서 item을 찾는다.
            if curNode == None:
                print("item not found")
            elif curNode.item == item:
                # 찾은 item을 리턴한다.
                return curNode
            elif item < curNode.item:
                # 최종적으로 찾은 item을 리턴해야 한다. 리턴이 없으면 찾아도 리턴되지 않으므로 재귀를 끝낼때 리턴에 의해 item을 연쇄적으로 반환해야 한다.
                return self._search(curNode.left, item)
            elif item > curNode.item:
                # 최종적으로 찾은 item을 리턴해야 한다.
                return self._search(curNode.right, item)
            
        def inOrder(self):
            return self._inOrder(self.root, [])
    
        def _inOrder(self, node, sorted=[]):
            # 현재 노드가 비어있지 않으면 일단, 계속 좌측으로 간다. 좌측의 끝에 도달하면 노드를 출력하고 오른쪽으로 이동한다.
            if node is not None:
                self._inOrder(node.left, sorted)
                sorted.append(node.item)
                self._inOrder(node.right, sorted)
            return sorted
    
    a = [50, 30, 80, 10, 40, 90]
    t = BSTree()
    for val in a:
        t.insert(val)
    
    t.insert(35)
    print(t.search(40).item)

• 트리 최소값 찾기 알고리즘
  • 루트 부터 왼쪽 노드로 이동한다. 이동하는 도중에 None을 만나면 None의 부모노드가 최소값을 가진 노드이므로 부모노드 값을 리턴한다.
  • 최소노드 삭제 알고리즘
    • 아래 그림처럼 왼쪽으로 내려가면서 curNode.left가 None이면 curNode.right를 리턴하여 curNode에 저장한다. 

      

    • 삭제 알고리즘
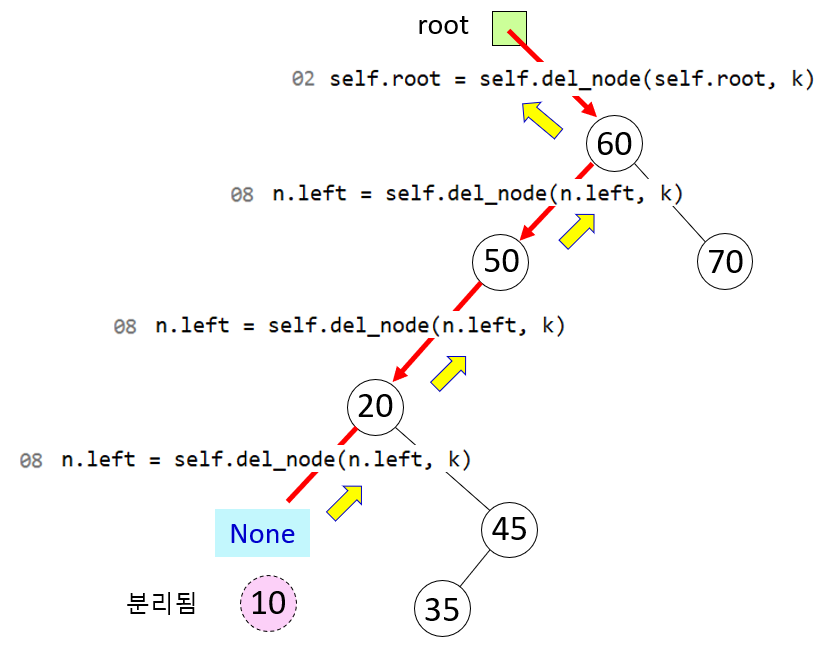
      • 루트노드부터 삭제노드를 찾는다. 10을 삭제한다고 하자.
      • 삭제가 노드가 없으면 현재노드가 None이 되고 None를 리턴한다.
      • 삭제노드를 찾았을 때, 삭제노드가 자식이 없는 경우와 하나 있는 경우, 그리고 둘이 있는 경우가 있다.
      • 자식이 없으면 해당노드만 삭제하면 된다. 아래 그림에서 10을 삭제한다고 하면 10대신 None을 리턴한다.
      • 
      • 자식이 하나 있으면 자식이 후계노드가 된다.
      • 자식이 하나 이하이고, 삭제node.right == None 이면 삭제node.left를 리턴한다. 삭제node.right == None인 경우는 오른쪽만 None인 경우와 오른쪽, 왼쪽 둘 다 None인 경우가 있다. 이 경우는 삭제노드 자리에 삭제node.left가 저장된다.
        • 아니고 삭제node.left == None 이면 삭제node.right를 리턴한다. 35를 삭제하는 경우, 왼쪽만 None인 경우로 리턴값 삭제node.right가 삭제노드 자리에 들어간다. 
        • 자식이 둘이 있으면 오른쪽에서 최소노드 혹은 왼쪽에서 최대노드가 후계노드가 된다.
          • 아래 그림에서 target = 20 이 삭제 노드다.
            Step 1: target 우측에서 최소노드를 찾는다.(최소노드는 삭제노드와 가장 유사한 노드다.)
            Step 2: 최소노드를 target으로 올리기 위해 최소노드의 우측에 target의 우측인 45 노드를 지정한다.
            Step 3: 최소노드의 좌측에는 target의 좌측인 10 노드를 지정한다.
            Step 4: 재귀를 끝내기 위해 최소노드를 삭제대상 노드의 자식노드로 리턴한다.
            

            

            class BSTree:
                def __init__(self):
                    self.root = None
            
                def insert(self, item):  # item을 삽입한다.
                    self.root = self._insert(self.root, item)
            
                def _insert(self, curNode, item):
                    # curNode 부터 밑으로 item 삽입위치를 찾아 삽입한다.
                    # 현재 노드가 None이면 현재노드에 새노드를 삽입한다.
                    if curNode == None:
                        curNode = BNode(item)
                    elif item < curNode.item:
                    # 삽입할 값이 현재 노드값 보다 작으면 좌측을 현재노드로 보고 삽입을 실행한다.
                        curNode.left = self._insert(curNode.left, item)
                    else:
                    # 삽입할 값이 현재 노드값 보다 크면 우측을 현재노드로 보고 삽입을 실행한다.
                        curNode.right = self._insert(curNode.right, item)
                    # 재귀가 끝나서 새노드를 삽입했다면 자신을 호출한 프로세스에 새노드를 리턴한다.
                    return curNode
            
                def search(self, item):
                    # 루트부터 item을 찾는다.
                    return self._search(self.root, item)
            
                def _search(self, curNode, item):
                    # curNode 밑에서 item을 찾는다.
                    if curNode == None:
                        print("item not found")
                    elif curNode.item == item:
                        # 찾은 item을 리턴한다.
                        return curNode
                    elif curNode.item > item:
                        # 최종적으로 찾은 item을 리턴해야 한다. 리턴이 없으면 찾아도 리턴되지 않으므로 재귀를 끝낼때 리턴에 의해 item을 연쇄적으로 반환해야 한다.
                        return self._search(curNode.left, item)
                    elif curNode.item < item:
                        # 최종적으로 찾은 item을 리턴해야 한다.
                        return self._search(curNode.right, item)
            
                def inOrder(self):
                    return self._inOrder(self.root, [])
            
                def _inOrder(self, node, sorted=[]):
                    # 현재 노드가 비어있지 않으면 일단, 계속 좌측으로 간다. 좌측의 끝에 도달하면 노드를 출력하고 오른쪽으로 이동한다.
                    if node is not None:
                        self._inOrder(node.left, sorted)
                        sorted.append(node.item) 
                        self._inOrder(node.right, sorted)
                    return sorted
            
                def levelOrder(self, node=None):
                    if node == None:
                        node = self.root
                    h = self.height(node)
                    for i in range(1, h + 1): # Level 1, 2, ... 순으로 내려가면서 
                        self._levelOrder(node, i)
                        print()
            
                def _levelOrder(self, node, level):
                    if node is None:
                        return
                    if level == 1:
                        print(node.item, end=" ")
                    elif level > 1: # 하나씩 내려가면서 level을 낮춘다. level이 1이 되는 순간 프린트
                        self._levelOrder(node.left, level - 1)
                        self._levelOrder(node.right, level - 1)
            
                def height(self, node):
                    if node is None:
                        return 0
                    else:
                        # Compute the height of each subtree
                        lheight = self.height(node.left)
                        rheight = self.height(node.right)
            
                        # Use the larger one
                        if lheight > rheight:
                            return lheight + 1
                        else:
                            return rheight + 1
            
                def minimum(self):
                    # 트리의 최소값을 찾는다. 최소값은 왼쪽 None을 만났을 때 부모노드의 값이다.
                    return self._minimum(self.root.left, self.root)
            
                def _minimum(self, node):
                    if node.left != None:
                        return self._minimum(node.left)
                    else:
                        return node
            
                def delMin(self):
                    # 최소값을 가진 노드를 삭제한다.
                    self.root = self._delMin(self.root)
            
                def _delMin(self, node):
                    # 현재 노드 좌측이 None면, 현재노드가 최소값이고 현재 노드 우측값이 현재노드를 제거했을 때 최소값이므로 부모노드의 왼쪽에 리턴한다.(p 152 그림 5-9, 5-10)
                    # 만약 리턴된 node.right 역시 None이라면 즉, 최소노드의 자식노드가 모두 None이라면 부모노드의 왼쪽에 None이 리턴된다.
                    if node.left == None:
                        return node.right
                    node.left = self._delMin(node.left)
                    return node
            
                def delete(self, item):
                    self.root = self._delete(self.root, item)
            
                def _delete(self, node, item):
                    if node == None: # 끝까지 가면 None을 리턴한다.(못찾았다)
                        return None
                    if node.item > item: # 삭제노드가 왼쪽에 있다면
                        node.left = self._delete(node.left, item)
                    elif node.item < item: # 삭제노드가 오른쪽에 있다면
                        node.right = self._delete(node.right, item)
                    else: # 삭제노드를 찾았다면
                        if node.right == None:
                            return node.left # 삭제노드 위치에 삭제노드의 좌측노드를 리턴한다.(좌측노드가 비어 있을 수도 있음)
                        elif node.left == None:
                            return node.right  # 삭제노드 위치에 삭제노드의 우측노드를 리턴한다.(우측노드는 비어 있지 않음)
                        # 삭제노드의 자식이 둘 다 있다면 삭제 노드 우측에서 최소노드를 후계자로 지정하고 밑에 있는 후계자노드는 삭제한다.
                        delNode = node
                        node =  self._minimum(delNode.right)     # 삭제노드 우측에서 최소노드를 찾아 삭제노드와 바꾼다.
                        node.right = self._delMin(delNode.right) # 우측에서 최소노드를 지운다.
                        node.left = delNode.left                 # 삭제노드 좌측을 후계노드에 이어준다.
                    return node
            
            nodes = [60, 50, 70, 20, 10, 45, 35, 25, 30, 40]
            
            t = BSTree()
            for i in range(len(nodes)):
                t.insert(nodes[i])
            
            print(t.levelOrder())
            
            #t.delete(10)
            t.delete(20)
            print(t.levelOrder())​

          • AVL Tree
          • Red Black Tree
          • B Tree