Dijkstra 알고리즘
- BFS를 사용하여 최소거리 경로를 찾을 수 있다.
- 다익스트라 알고리즘은 최소 Cost를 가지는 경로를 찾을 수 있는 알고리즘이다.
- 여기서, Cost는 시간일 수도 있고, 시간, 신호등 수, 주변 경관 등을 적절하게 점수화 한 것일 수도 있다.
(예를 들어, 시간이 오래 걸리거나 신호등이 많거나 차선이 좁으면 상승하는 Cost 함수를 만들 수 있다면 이 Cost 함수를 최소화 하는 경로를 찾을 수 있다는 의미이다.) - 이를 이용하면 네비게이션 알고리즘에서 최단경로, 최소시간, 최소비용, 최적 경로라는 이름으로 경로를 탐색하고 사용자는 이 중 적절한 경로를 선택하도록 하는 것이 가능하다.
- 다익스트라 알고리즘은 현재노드를 통해 연결된 노드로 가는 것과 다른 경로를 통해 가는 Cost를 비교하여 더 작은 Cost가 있을 경우, 업데이트하는 방법이다.
- 아래의 그림에서 A로 가는 방법은 start에서 A로 가는 방법과 start -> B -> A의 방법이 있고 이 중 후자가 더 빠르다.

- 위 그래프를 딕셔너리에 저장해보자.
- Step 0: nodes에서 최소거리 노드를 찾는다. 처음에는 시작점의 거리가 0이고 나머지는 inf 이므로 시작점이 현재 노드가 된다.
- Step 1: 현재 노드를 방문한것으로 처리한다.
- Step 2: 현재노드의 이웃노드를 구하고 현재노드를 통해 이웃노드로 가는 비용과 이 노드를 거치지 않고 가는 비용을 비교하여 만약, 현재노드를 통해 가는 것이 작으면 비용과 부모노드를 업데이트 한다.
- Step 3: 방문하지 않은 노드들 중에 최소비용노드를 찾아 현재노드로 지정하고 Step 1으로 이동한다.
다익스트라 알고리즘
최단경로 탐색알고리즘 흔히 인공위성 GPS 소프트웨어 등에서 가장 많이 사용.
다익스트라 알고리즘은 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단경로를 알려줍니다.
이때 음의 간선 즉 간선의 비용이 음수일때는 존재하지 않기 때문에,
다익스트라는 현실세계에 사용하기 좋은 알고리즘입니다.
기본적으로 그리디 알고리즘으로 구분되는 데, 매번 '가장 비용이 적은 노드'를 선택해서
임의의 과정을 반복해야 하기 때문이다.
즉 현재까지 알고 있던 최단 경로를 계속해서 갱신하는 알고리즘.
1. 출발노드를 설정합니다.
2. 출발노드를 기준으로 각 노드의 최소비용을 저장합니다.
3. 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택합니다.
4. 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소비용을 갱신합니다.
5. 위 과정에서 3번~4번을 반복합니다.
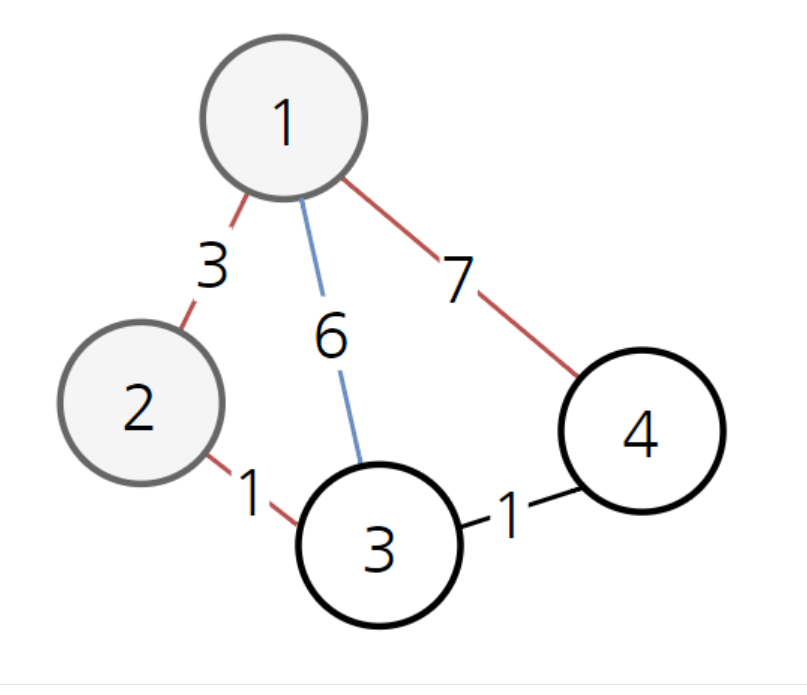
위와 같이 나중에 컴퓨터는 경로 1->3의 비용이 6인데 반해, 경로 1-2-3이 총 비용 4보다 더 저렴하다는 것을 알게 된 후, 현재까지 알고 있던 3으로 가는 최소비용 6을 새롭게 4로 갱신하여 제시합니다.
다시 말해, 다익스트라 알고리즘은 '현재까지 있던 최단 경로를 계속해서 갱신'해서 제공하는 알고리즘 입니다.
실제로 컴퓨터 안에서 사용할 때는 이차원 배열을 사용. [인접리스트를 활용한 구현방식 사용]
https://m.blog.naver.com/ndb796/221234424646
23. 다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra) 알고리즘은 다이나믹 프로그래밍을 활용한 대표적인 최단 경로(Shortest Path) 탐...
blog.naver.com
https://www.youtube.com/watch?v=611B-9zk2o4
네비게이션 알고리즘 - 데이크스트라 알고리즘
데이크스트라 알고리즘(영어: Dijkstra algorithm) 또는 다익스트라 알고리즘은 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘
내비게이션의 경로 탐색은 ‘데이크스트라 알고리즘’을 기반으로 한다.
짧게 요약하면 두 꼭짓점 간의 최단 경로를 찾는 알고리즘이다.
데이크스트라 알고리즘의 핵심은 교차점마다 시작점과의 거리 값을 부여하고 이때 가장 짧은 거리의 경로만을 남겨둠으로써 최단 거리를 계산하는 것이다. 이때 교차점은 지도 DB로 환산하면 특정 건물이나 블록 등이 되겠다.
어쨌든 이렇게 구성된 ‘최단 경로’는 같은 원리의 알고리즘을 기반으로 했기 때문에 결과는 하나일 수밖에 없다.
Q 그런데도 내비게이션 앱마다 경로가 달라지는 이유가 뭘까.
내비게이션 경로 탐색을 이루는 다양한 ‘고유의 알고리즘’이 적용됐기 때문이다. 여기에는 실시간 교통 정보나 고속도로 및 국도 전용도로 선택 여부, 유료 도로 여부, 교통 신호나 과속 단속 구간 등이 포함된다.
내비게이션 앱들은 경로 탐색에 영향을 미치는 이와 같은 요인들에 가중치를 둠으로써 ‘최적 경로’를 도출한다.
앱마다 가중치를 두는 요인이 모두 다르기 때문에 추천 경로가 다를 수밖에 없는 것이다.
우선 내비게이션 앱 중 가장 많은 유저를 거느리고 있으면서, 만족도 역시 높은 티맵부터 살펴보자. 티맵이 제안하는 출발지에서 목적지까지의 ‘최적길’은 18km 거리에 45분이 소요되는 경로다. 전반적으로 운전자가 굳이 돌아가야 하는 구간 없이 군더더기 없는 경로를 추천해준다. 큰 길로 진입하기 위해 먼 길을 가게 하는 것보다, 좁은 골목길을 뚫고 가장 최단 거리를 가게 하는 특징이 있었다.
네이버 지도가 제안하는 출발지에서 목적지까지의 ‘가장 빠른 추천 경로’는 21km 거리에 50분이 소요되는 경로다. 앞서 말한 티맵과는 달리 큰 길에 진입하기 위해 다소 불필요한 거리를 주행하게 하는 경향이 있었다. 대신 경로를 자세히 보면 이면 도로와 같은 사고 위험이 많은 길을 피해 가려는 특징이 있다. 운전자가 운전하기 가장 편한 길을 안내하기 때문에 초보 운전자들에게는 유용하겠다 싶었다.
마지막으로 카카오내비는 티맵과 네이버 지도의 중간 지점에 있는 듯 보인다. 카카오내비가 제안한 출발지에서 목적지까지의 ‘추천경로1’은 19km 거리에 48분이 소요되는 경로다. 전반적으로 티맵과 비슷하게 최단 거리를 제안하고 있는 듯 하나, 교통 정보상 정체 구간은 피해 가는 경로를 택했다. 결과적으로 티맵보다 1km 멀고 3분이 더 소요되긴 하지만, 정체보다는 서행이 낫다고 판단된다면 카카오내비를 선택할 듯싶다.
티맵, 카카오내비, 네이버 지도 모두 전반적으로는 비슷하지만
분명히 다른 길을 추천 경로로 제안하고 있다는 점에서 각자 다른 요인을 가중치로 두고 있다는 점은 확실하다. 이번 테스트에서는 티맵의 경우 최단 거리, 네이버 지도는 편한 길, 카카오내비는 교통 정보 반영을 가중치로 두고 경로를 안내했다.
자동차 네비게이션 길찾기 알고리즘은 어떻게 만들어졌을까?
지방에서 서울로 올라오는데, 네비게이션이 문제를 일으킨다. 그러다가 과연 네비게이션의 길찾기 기능을 어떠한 알고리즘으로 만들어졌을까 궁금해진다. 기본적으로 아주 간단한 길찾기라면
danbis.net
기본적으로 도로별로 등급을 매긴다고 하고, 등급별로 우선순위를 두어서 높은 등급을 우선적으로 추천해주는 방식이라고 한다.
고속도로 > 자동차전용도로 > 국도 > 지방도로 > 골목길 뭐 이런 수준으로 생각
H.W #11 : 다익스트라 알고리즘으로 지하철 최단 경로를 구하시오.
(1) 먼저, 위 코드를 클래스로 만들어 재사용 가능하도록 개발하시오.
(class dijkstra 이름으로 개발하고 setEdge(self,a,b,w), getPath(self,start,end) 메소드를 구현하세요)
(2) subway.csv 파일에서 원하는 경로에 대한 최소비용 경로를 계산해보세요.
def _neighbor(curNode):
# curNode에 연결된 이웃노드를 리스트로 리턴한다.
neighbor = {}
for edge in graph:
if edge[0] == curNode:
neighbor[edge[1]]= edge[2]
elif edge[1] == curNode:
neighbor[edge[0]] = edge[2]
return neighbor
def _getWeight(n1, n2):
# 그래프에서 노드 n1, n2의 가중값을 리턴한다.
for edge in graph:
if edge[0] == n1 and edge[1] == n2:
return edge[2]
elif edge[0] == n2 and edge[1] == n1:
return edge[2]
return None
def dicFilter(cost, nodes):
import sys
mini = sys.maxsize
for key, value in cost.items():
if key in nodes:
if value[0] < mini:
mini = value[0]
curNode = key
return curNode
while True:
visits.add(curNode)
nodes.remove(curNode)
neighbors = _neighbor(curNode)
# 모든 이웃에 대해 현재 노드를 통해 이웃노드에 접근하는 cost가 더 작을 경우, cost 값을 갱신하고 부모노드를 변경한다.
for node in neighbors:
if cost[curNode][0] + _getWeight(curNode,node) < cost[node][0]:
cost[node][0] = cost[curNode][0] + _getWeight(curNode, node)
cost[node][1] = curNode
if len(nodes) > 0:
curNode = dicFilter(cost, nodes)
else:
break
path = [end]
while end != start:
path.append(cost[end][1])
end = cost[end][1]
print(path[::-1])
https://justkode.kr/algorithm/python-dijkstra
Python으로 다익스트라(dijkstra) 알고리즘 구현하기
최단 경로 알고리즘은 지하철 노선도, 네비게이션 등 다방면에 사용되는 알고리즘입니다. 이번 시간에는 Python을 이용해 하나의 시작 정점으로 부터 모든 다른 정점까지의 최단 경로를 찾는 최
justkode.kr
https://can-do.tistory.com/162
[Graph] 최단경로검색, Dijkstra algorithm(다익스트라)
Dijkstra algorithm(다익스트라 알고리즘) 열심히 그렸는데, 맞겠지. stack에 값을 넣어놓고 pop해서 꺼내면 된다. *A에서 D로 가는 경우, A에서 B를 거쳐 D로 가게되면 8이 됨으로, 7A를 저장해 준다. 1 2 3
can-do.tistory.com
Class dijkstra
def __init__(self, name):
self.name = name
self.neighbors = []
def add_node(self, value):
self.nodes.add(value)
def add_edge(self, from_node, to_node, distance):
self._add_edge(from_node, to_node, distance)
self._add_edge(to_node, from_node, distance)
def _add_edge(self, from_node, to_node, distance):
self.edges.setdefault(from_node, [])
self.edges[from_node].append(to_node)
self.distances[(from_node, to_node)] = distance
def _neighbor(curNode):
neighbor = {}
for edge in graph:
if edge[0] == curNode:
neighbor[edge[1]]= edge[2]
elif edge[1] == curNode:
neighbor[edge[0]] = edge[2]
return neighbor
def dijkstra(graph, initial_node):
visited = {initial_node: 0}
path = {}
nodes = set(graph.nodes)
while nodes:
min_node = None
for node in nodes:
if node in visited:
if min_node is None:
min_node = node
elif visited[node] < visited[min_node]:
min_node = node
if min_node is None:
break
nodes.remove(min_node)
cur_wt = visited[min_node]
for edge in graph.edges[min_node]:
wt = cur_wt + graph.distances[(min_node, edge)]
if edge not in visited or wt < visited[edge]:
visited[edge] = wt
path[edge] = min_node
return visited, path
def shortest_path(graph, initial_node, goal_node):
distance, path = dijkstra(graph, initial_node)
route = [goal_node]
while goal_node != initial_node:
route.append(path[goal_node])
goal_node = path[goal_node]
route.reverse()
return routehttps://fullyalive.tistory.com/45
[파이썬 예제] 지하철 최단 경로 찾기
from collections import deque # 지하철역 클래스 class Station: def __init__(self, name): self.name = name self.neighbors = [] def add_connection(self, another_station): self.neighbors.append(another..
fullyalive.tistory.com
Class dijkstra
def __init__(self, name):
self.name = name
self.neighbors = []
def add_connection(self, another_station):
self.neighbors.append(another_station)
another_station.neighbor.append(self)
def _neighbor(curNode):
# curNode에 연결된 이웃노드를 리스트로 리턴한다.
neighbor = {}
for edge in graph:
if edge[0] == curNode:
neighbor[edge[1]]= edge[2]
elif edge[1] == curNode:
neighbor[edge[0]] = edge[2]
return neighbor
def bfs(start, goal):
previous = {}
queue = deque()
current = None
previous[start] = None
queue.append(start)
while len(queue) > 0 and current != goal:
current = queue.popleft()
for neighbor not in previous.key():
if neighbor not in previous.keys():
queue.append(neighbor)
previous[neighbor] = current
if current == goal:
path = [goal]
x = goal
while previous[x] != None:
x = previous[x]
path.append(x)
return path
return Nonefrom collections import deque
# 1- station 클래스를 만듭시다.
class Station:
# 초기값 설정 생성자를 통해 인스턴스 변수들을 생성, 설정해 줍니다.
def __init__(self, name):
self.name = name
# 이웃 역들을 담고 있는 리스트
self.neighbor = []
def add_connection(self, another_station):
self.neighbor.append(another_station)
another_station.neighbor.append(self)
# 2- 파일 읽기
# station 사전 만들기 - station 사전을 만드는 이유는 각각의 역 이름과 각 역에 담긴 정보들(Station 클래스의 인스턴스)을 key - value 값으로 입력하기 위함입니다.
stations = {}
# station 파일을 읽어봅시다.
in_file = open("stations.txt")
# add_connection 메소드를 활용하기 위해 이전 역과 현재 역으로 구분 시켜줄 필요가 있습니다.
# 물론, 현재 이전역은 없는 상태이므로 None으로 지정해줍니다.
previous_station = None
for line in in_file:
temporary_line = line.strip().split(" - ")
# 리스트를 각각의 역으로 변환시키고, 공백을 없애주기 위해 이중 반복문을 활용합시다.
for line in temporary_line:
station_line = line.strip()
# current_station을 현재역의 정보를 담고있는 인스턴스 값으로 지정해줍니다.
current_station = Station(station_line)
# 각각의 역의 이름을 stations 사전의 key값으로 입력하는게 목적이었으므로
# 아래와 같이 코드를 작성합니다.
if station_line not in stations.keys():
# 현재 역의 이름을 key값으로, 그 역의 정보(인스턴스)를 value로 저장합니다.
stations[station_line] = current_station
# 각 호선당 중복되는 역(환승 역)일 경우 에러가 발생하므로 경우를 나눠줘야 합니다.
# 현재역은 이전에 정해줬던 역의 value값임을 선언해줘야
# 자동 환승을 합니다. station[station_line] = current_station 으로 지정 할 경우
# 환승하지 않습니다!
elif station_line in stations.keys():
current_station = stations[station_line]
# 이전 역과 현재 역을 이웃역으로 엮어줘야 하나, 현재 이전 역은 None 이므로, 아래와 같이 조건문을 활용합니다.
if previous_station != None:
current_station.add_connection(previous_station)
# 반복문을 돌면서 모든 역을 사전에입력시켜줘야 하므로 아래와 같이 코드를 작성합니다.
previous_station = current_station
in_file.close()
# 3 - bfs 알고리즘 생성
def bfs(start, goal):
# previous 사전의 역할은 각각의 역을 key - value 관계로 이어주는 것입니다.
previous = {}
queue = deque()
# 현재 확인하고 있는 역은 없으니 None값으로 지정합니다.
current = None
# 현재 시작역과 연결된 역은 없다는 뜻입니다.
previous[start] = None
# 목표 역에 도달할때까지 queue를 통해 확인해야 하므로 시작역을
# 확인열에 집어넣습니다.
queue.append(start)
while len(queue) > 0 and current != goal:
# 여기서 current는 목표 역이 아니라고 판명된(queue 확인열을 통해) 역으로 지정됩니다.
# 여기서 None값을 탈출하는 것이죠!
current = queue.popleft()
for neighbor in current.neighbor:
# previous 사전을 만든 이유를 다시 봐야 합니다.
# 각각의 역을 이웃지어 주는 역할이므로, 이웃역이 사전에 없을 경우 아래와 같은 식으로 코드를 작성합니다.
if neighbor not in previous.keys():
# 아직 확인을 하지 않은 역이므로 확인열에 넣고,
queue.append(neighbor)
# 사전에 추가합니다.
previous[neighbor] = current
if current == goal:
# 경로를 만들어야 하는데 여기서 가장 적합한 툴은 리스트입니다.
# 그러므로 리스트를 통해 경로를 작성해봅시다.
path = [goal]
# 다시 한 번, previous 사전의 역할을 생각해봅시다.
# previous 사전은 각각의 역을 K - V 관계로 엮어주는 것이죠?
# 고로 아래와 같이 목표역(goal)에 해당하는 value(이웃 역)이 있을 경우 경로를 만들 수 있기 떄문에
# 아래와 같이 코드를 작성합니다. 다만 역 순서가 역순(reverse)으로 출력되니
# 필요할 경우 reverse 메소드를 활용할 수 있겠네요!
while previous[goal] != None:
# goal을 목표역과 이웃된 역으로 재지정해줍니다.
goal = previous[goal]
path.append(goal)
return path
# 사전에 있는 모든 역을 확인했음에도 목표역을 찾지 못한 경우입니다.
if current != goal:
return None
# 테스트
start_name = "이태원"
goal_name = "잠원"
start = stations[start_name]
goal = stations[goal_name]
path = bfs(start, goal)
for station in path:
print(station.name)'프로그래밍 공부 > 알고리즘 공부' 카테고리의 다른 글
| 정렬 알고리즘 (시간복잡도 비교) (0) | 2022.10.27 |
|---|---|
| 플로이드 워셜, 다익스트라 알고리즘 (1) | 2022.10.08 |
| 알고리즘 정리 DFS, BFS, MST(최소비용신장트리) (0) | 2021.05.28 |
| Chapter 10 다양한 알고리즘 (0) | 2021.01.08 |
| Chapter 09. 최단경로 (0) | 2021.01.05 |



댓글